FAQ
EUCLIDEA: GENERAL
There are no built-in solutions in Euclidea. The app just verifies that the target object is present on the screen.
Most probably your solution is not accepted because it is just an approximation. To check this you can:
-
Read carefully the statement of the problem. To review it tap a preview card in the top left corner of the game screen. You can also review definitions in our glossary by tapping "?" under the statement.
-
Make sure that the required object is really constructed. For example, you could forget to set a point in one of the ends of a line segment.
-
Select the Hand tool and try to drag different points. A correct construction should satisfy the statement of the problem for any configuration of points and figures.
-
Check the red points. They are not fixed and can be moved. In general, you do not need to avoid them since some optimal solutions are impossible without red points. But, for example, a midpoint or a tangent point can never be red.
-
Switch to the Explore mode (the orange button) and take a look how the answer depends on point configuration. Compare this with your solution.
-
Try to prove that your construction satisfies the statement of the problem. It is not enough if it just visually coincides with the correct answer.
-
If nothing helps, please write us at support@euclidea.xyz.
Each solution is scored in two types of moves: L (straight or curved lines) and E (elementary Euclidean constructions). Points are not taken into account.
L counts tool actions: constructing a line, a perpendicular, and so on. E counts moves as if a construction was made with real compass and straightedge. Each advanced tool has its own E cost (see table).
The goal is to solve a problem using the minimum number of moves. L and E goals can be satisfied independently. A lot of problems have universal solution that satisfies both goals. But some problems should be solved twice: one solution to reach L goal and another solution to reach E goal.
If there are several objects satisfying the statement of a problem, you can get a hidden V-star by constructing all of them on the same screen. For example, given a side, it is possible to construct two squares (V-star is available) while given a diagonal, the square is unique (no V-star!). In most cases it is enough to use reflection or another kind of symmetry.
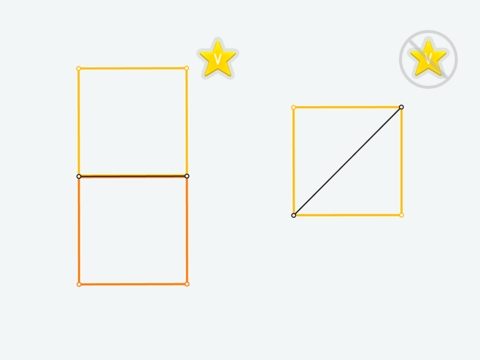
Useful hints:
-
Carefully read the statement. For example, if a diagonal is mentioned there, consider using different diagonals.
-
Check the intersection points that are used in your construction. A circle usually produces a pair of intersection points with a line or another circle. You can try using both of them.
-
Some problems have 3 or even 4 answers. If your second answer is accepted (highlighted in orange) but V-star does not appear, you should continue searching for more answers and construct them.
-
There is a V-star hint in the game. It shows the number of possible answers on the current level. Open Menu in the top right corner on the game screen (3 lines button), then tap bulb, and choose V-star.
Tap the Menu (hamburger) button in the top right corner of the game screen, then on a right arrow.
To switch the language in the Euclidea app:
- On the start screen tap the cogwheel button.
- In the Settings dialog tap the second menu item.
- Select needed language in the list and tap the bottom button to apply it.
You can transfer your game progress (earned stars and saved solutions of the problems) between devices using the same Euclidea account. Log in to prevent losing your results.
Euclidea is a game. It is a challenge. Its goal is to force users to think and explore geometry.
We suppose that it is much more pleasure to find a solution of the problem by yourself than to get the answer from someone else. So we do not provide complete solutions but can only give hints.
If you want to proceed after the first 2 packs without in-app purchase, please make sure that you have 74 stars totally. There are hidden V-stars in the game. (See How to find hidden V-stars?)
Note: After you have purchased the Unlock packs, stars are not taken into account anymore. The next problem is opened as you solve the previous one. You can also skip any level by tapping the Next button in the menu.
There are several methods to play Euclidea for free.
On a mobile device (iOS/Android):
- Solve each problem at the maximum score. You will need to earn all L, E, and V stars. It is hard but not impossible.
- Ask for a promo code. If you love geometry but cannot buy the in-app purchase, write us at support@euclidea.xyz.
On a desktop:
- Play web version of the game. It has no restrictions on number of stars.
Android: You can use the standard Back button. To bring the navigation buttons back just swipe up from the bottom. This is a commonly used way as it is written in Android Quick Start Guide.
Points are not counted. Any other tool which actually produces a line or a circle costs 1L. E-cost is individual:
Hint. E-cost of the selected tool is displayed as small marks in the top left corner of its button.
Euclid originally used a "collapsible" compass that did not keep the measured distance. So we follow the tradition and it corresponds to our Circle tool. The Compass tool becomes available in the Zeta pack.
The in-app purchases should be automatically restored if you use the same Google account or Apple ID on your new device. Though, your progress is lost and you need to solve the problems again (maybe, not at the perfect score). But you can skip any problem by tapping the Next button in the menu (a 3-lines button).
iOS: To restore your purchases tap Settings -> Purchases -> Restore purchases.
We understand the importance of your privacy and data security. If you wish to delete your Euclidea account and associated data, please follow the steps outlined below. This action will remove your personal information from our servers and terminate your account access.
How to Request Account Deletion:
- Send an Email Request:
- Compose an email to support@euclidea.xyz with the subject line "Request for Account Deletion".
- Include your account details (e.g., username or email address linked to your account) to verify ownership.
- Confirmation:
- Once we receive your request, we will send you an email to confirm that you want to proceed with the deletion. This is to ensure the security and ownership of the account.
- Reply to the confirmation email to proceed with the deletion.
- Processing Your Request:
- After receiving your confirmation, we will process the deletion of your account and associated data. You will receive a final email notification once this process is completed.
Data Deletion Details:
-
Types of Data Deleted: All personal data including but not limited to your progress, solutions, and any personal information will be permanently deleted from our servers.
-
Data Retention: Some non-personally identifiable data may be retained for analytical purposes to improve our app, but it will not be linked to your deleted account.
-
Retention Period: Any requests for data deletion will be honored within 30 days from the date of confirmation.
Should you have any further questions or require assistance with the process, please do not hesitate to contact us at support@euclidea.xyz.
EUCLIDEA: TYPICAL MISTAKES
A common error for level "Equilateral Triangle" is that the construction contains red points that are not fixed and can be moved. You can check it by using the Move (Hand) tool. To pass this level try to tap points instead of dragging. Or drag your finger directly to a point until it snaps.
Correct
Incorrect
When using Perpendicular Bisector Tool the dashed line connecting two points is not a line but just a decoration. It cannot be used for constructions.
Incorrect construction
The red point is not fixed and can be moved.
Note that a rhombus is a quadrilateral with four equal sides.
A common error for level 1.5 "Rhombus in Rectangle" is assuming that the angle of the rhombus is 60 degrees.
You can switch to the Explore mode (the orange button), reproduce your steps, and drag the top left corner of the rectangle using the Hand tool. A correct construction satisfies the statement of the problem for any configuration.
To solve the problem you can recall that a diagonal of a rhombus is the perpendicular bisector of its other diagonal.
Incorrect construction
In level 1.7 "Inscribed Square" the given point (it is black) should be one of the vertices of the square.
Incorrect construction

Do not try to guess a line that looks similar to the answer. Most probably, you will get just an approximation.
You can find a key to the solution if you drag the given point in the Explore mode. What is the pattern of the orange line (the answer) behavior?
Incorrect construction
EUCLIDEA: TIPS & TRICKS
L and E goals are independent. To get all stars at level 1.6 "Circle Center" you should solve it twice using different approaches: one solution with 2L and one more solution with 5E.
To find 5E solution in 1.6, try to construct perpendicular bisectors with circles and lines (without special tools). Then, you will see that it is possible to get rid of one circle.
The sequence of tools for this solution: OOO// (3 circles, then 2 straight lines).
You can complete the level 1.7 "Inscribed Square" with the sequence of tools: OO///// (2 circles, then 5 straight lines).
-
The first move a circle is the only possible.
-
The second move should give you the bottom vertex.
-
Last 4 moves are the sides of the square.
So you need to guess what the third move is. This move should give you some point on the side or its continuation. The easiest way to find it is to use the Explore mode (the orange button).
The idea of 2.2 is similar to 1.6 ("Circle Center"): you construct two angle bisectors by sharing the same circles. All the circles will have the same radius.
To solve problem 2.6 "Drop a Perpendicular" with 3E, you can use the idea of symmetry. Construct the mirror image of the given point across the line (two circles) and then connect them.
To complete level 2.7 Erect a Perpendicular with 1L 4E you should use only one tool. Try to figure out which one. Note that right angle is a half of a straight angle.
To solve problem 2.7 "Erect a Perpendicular" with 3E, you can use the Thales' theorem.
The sequence of tools for this solution: O// (a circle and 2 straight lines).
To solve level 2.8 "Tangent to Circle at Point" with 3E use the sequence of tools OO/ (2 circles and a straight line). Please note that you do not need the center of the circle.
Level 4.1 "Double Segment" should be solved using only circles. That is the heart of the problem. It can be done in 3 moves. The first 2 circles are the only possible, so you need to find the third circle that will pass through the required point.
The sequence of tools is OOA (2 circles and an angle bisector). First, you can figure out how the last move works. It will give you a key to the first two moves. Note that the center of the first circle is not on the ray and not every point is suitable for it.
The trisection of an angle is not possible in general case, so you need to use that 54/3 = 18. You can also note that 90-54 = 36 = 2*18 and so on.
EUCLIDEA: SUGGESTIONS
Euclidea supports:
- English
- French
- German
- Italian
- Spanish
- Portuguese (Brazil)
- Greek
- Japanese
- Korean
- Chinese (Simplified)
- Russian
- Ukrainian
- Dutch
- Polish
- Slovak
If you want to help with translation to your native language, please write us at support@euclidea.xyz.
We considered a free workspace some time ago. It is possible but it does not look appropriate in Euclidea game. For example, there is lack of tools and no possibility to color objects. So we would prefer to create a separate app based on Euclidea engine where you can draw any constructions, save them, share, etc.
iOS: Try Euclidea: Sketches.
There are no exact plans on the eraser tool in Euclidea.
PYTHAGOREA: GENERAL
To skip levels in Pythagorea and Pythagorea 60° just tap the Next button (right arrow) several times until it is filled with color (see a video in our Instagram). The number of taps will increase each time you skip a level, so do not overuse.
PYTHAGOREA: HINTS
Some users are stuck on 1.13 because there is no way to construct a segment that goes through the required midpoint.
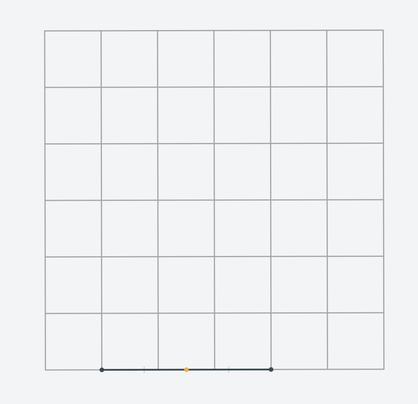
But it is possible to achieve this with a line. Note that pale gray rays extend any constructed segment to a line. For example, you can construct a vertical line that goes through the required midpoint. Note that it goes through the centers of the grid cells.
Bonus: try to solve 1.13 using just one auxiliary line.
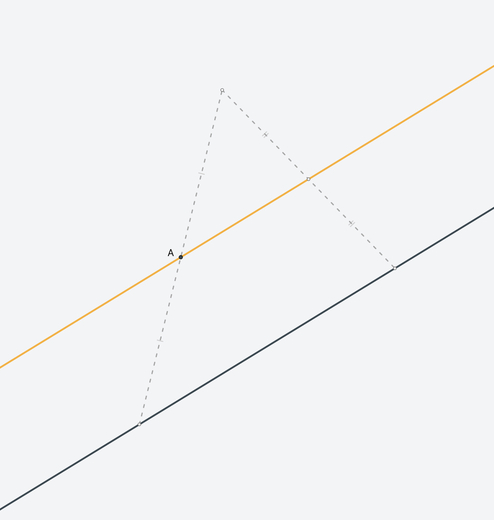
There are several ways to solve level 2.19.
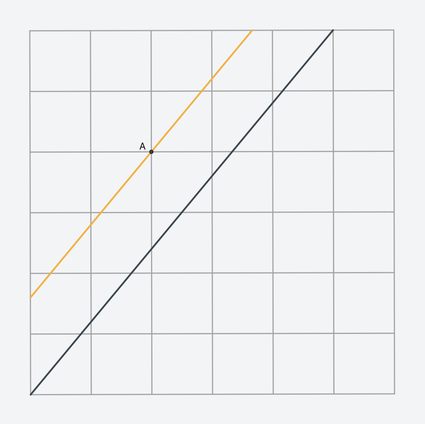
For example, you can apply the Intercept theorem by constructing a triangle for which the required line is a midline.
PYTHAGOREA: TYPICAL MISTAKES
In level 8.3 the fourth vertex of the trapezoid should be a grid node, that is a point of intersection of grid lines. You can find definitions of the terms used in the problem statement by tapping the "i" button on the game screen.
Incorrect
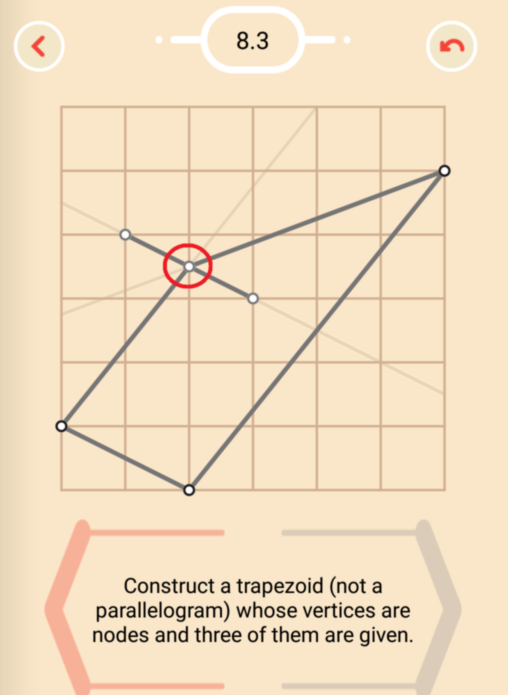
Note that trapeziod in Pythagorea is defined as a quadrilateral with two parallel sides. The other two sides are assumed to be not parallel. So the parallelogram is not accepted in this problem.
XSECTION: GENERAL
The Android version of XSection was released later and we implemented several new ideas in it. The tasks from the iOS version have been improved and rearranged, the application design has been completely updated.
Now there are no exact plans to update the iOS version.
XSECTION: TYPICAL MISTAKES
There is no bug in level 9.5. A diagonal section of a cube is a rectangle but not a square. That is why its diagonals are not perpendicular. Take a look at visualization of this problem in our Instagram.
Incorrect
